http://www.psiquiatriainfantil.com.br/congressos/uel2007/305.htm
http://www.psiquiatriainfantil.com.br/congressos/uel2007/305.htm |
|

Londrina, 29 a 31 de outubro de 2007 – ISBN 978-85-99643-11-2
DEFICIÊNCIA MENTAL E AQUISIÇÃO MATEMÁTICA: O CURRÍCULO
COMO REDE DE RELAÇÕES1
Rosana Ap. Salvador Rossit2
Universidade Federal de São Paulo
1 Trabalho desenvolvido com o apoio da FAPESP.
2 Terapeuta Ocupacional, Mestre e Doutora em Educação Especial pela Universidade Federal de São Carlos, Pós-Doutora pela UFSCar/Departamento de Psicologia/LAHMIEI.
RESUMO
O presente estudo tem como objetivo analisar a aquisição de relações matemáticas e apresentar o currículo utilizado
com deficientes mentais. O referencial teórico baseou-se na análise do comportamento e no currículo como rede de
relações. As inúmeras variáveis que controlam o comportamento matemático precisam ser estudadas de maneira
mais aprofundada para esclarecer e revelar os possíveis requisitos e seqüências envolvidos na aquisição desses
comportamentos. Há diversos elementos que são essenciais para a aquisição de habilidades com alto grau de
complexidade, como é o caso da matemática, como os conceitos de números, operações básicas, conceitos
monetários, conceitos relacionais, entre outros. A escassez de uma base científica sólida que compreenda e explique
o processo de aquisição de tais conceitos, em pessoas com deficiência mental, fez com que crescesse o interesse em
pesquisar sobre a aprendizagem matemática e o currículo como rede de relações condicionais.
INTRODUÇÃO
Discussões no âmbito da Educação Matemática apontam a necessidade de adequar o trabalho
escolar a uma nova realidade, marcada pela crescente presença da Matemática em diversos campos
da atividade humana. Essas discussões têm influenciado análises e revisões nos currículos3 de
Matemática (Brasil, 1998).
3 O termo “currículo” é entendido como a totalidade de situações de ensino-aprendizagem, que estimula o
desenvolvimento do aluno, levando-o à aquisição de conhecimentos, habilidades e atitudes.
A Matemática está presente em diversas situações do cotidiano. Atividades comuns tais como
marcenaria, cozinha, limpeza, escritório e supermercado requerem sistemas de contagem e a
habilidade de usar e reconhecer numerais. Além dos números serem a linguagem da medida, eles
também são necessários para os comportamentos adaptativos de encontrar um endereço, usar um
telefone, “ler” horas de um relógio, ou mesmo apreciar um jogo de futebol (Spradlin, Cotter, Stevens,
& Friedman, 1974, Rossit, 2003).
Para Teberosky e Tolchinsky (2002, p.257), “saber matemática é uma necessidade imperativa
numa sociedade a cada dia mais complexa e tecnológica, em que se torna difícil encontrar
setores em que este conteúdo não esteja presente”.
Embora existam muitos estudos na área da educação (Resnick, Wang & Kaplan,1973; Kahhale,
1993; Teberosky & Tolchinsky, 2002) e da análise do comportamento (Spradlin, et al., 1974;
Stoddard, Bradley, & McIlvane, 1987; Stoddard, Brown, Hurlbert, Manoli, & McIlvane, 1989;
Green, 1992; Carmo, 1997; Prado, 1995; De Lèon, 1998; Prado, 2001; Medeiros, Haydu, Carmo,
& Rossit, 2002; Monteiro, & Medeiros, 2002; Rossit, 2003; Araújo, 2004; Reimberg, 2005) sobre o
ensino de matemática, a questão de como as pessoas adquirem os conceitos matemáticos ainda
requer investigações.
As inúmeras variáveis que controlam o comportamento matemático precisam ser estudadas de
maneira mais aprofundada para esclarecer e revelar os possíveis requisitos e as seqüências envolvidas
na aquisição de novos comportamentos. A escassez de investigações científica sólida que explique e
forneça subsídios para a compreensão do processo de aquisição de tais conceitos fez com que
crescesse o interesse em pesquisar sobre a aprendizagem matemática.
A matemática é apontada como uma disciplina complexa a qual é responsável por altos índices de
dificuldades na aprendizagem. Somando-se a isso, as características das pessoas com deficiência
mental para a aquisição de habilidades complexas, vê-se a necessidade de se estudar detalhadamente
o processo de aquisição dos comportamentos matemáticos e a expansão do repertório sob o enfoque
da análise comportamental.
Para delinear um perfil curricular para o ensino de comportamentos matemáticos pressupõe-se a
presença de inúmeros componentes que se relacionam entre si. Diversos elementos que são requisitos
essenciais para a aquisição de habilidades com alto grau de complexidade, como é o caso da
matemática, estão envolvidos, como os conceitos de números, operações básicas, conceitos
monetários, conceitos relacionais de igual-diferente, mais-menos, antes-depois, maior-menor, entre
outros.
Rossit (2003a) explica que o comportamento matemático
“(…) é uma subdivisão do comportamento verbal que apresenta um vocabulário
aritmético, uma sintaxe, uma estrutura de equações e outros tipos de funções, e
de encadeamento como na contagem, que ocorre tanto na comunicação, como
no pensamento. Esse é um comportamento complexo, que pode ser dividido em
unidades funcionais menores. Essas unidades podem aparecer como palavras
ditadas, figuras, numerais e valores monetários impressos, conjuntos, expressões
verbais, expressões numéricas, equações, dinheiro, nomeação, contagem,
construção de respostas, entre outras” (p. 13).
O currículo de matemática das escolas, em geral, focaliza o domínio e aplicação dos conceitos
matemáticos, operações, fatos matemáticos e resolução de problemas. Embora essas unidades
possam inicialmente aparecer separadas em um programa de ensino, na prática, elas tornam-se
crescentemente interligadas, como resultado da complexidade das tarefas e da aplicabilidade
matemática.
Porém, nas escolas, o conhecimento ainda é interpretado como uma cadeia de raciocínios, que se
articulam linearmente (Pires, 2000). A linearidade, que se concretiza numa sucessão de tópicos que
devem ser apresentados numa certa ordem, conduz a uma prática educativa fechada, em que há
pouco espaço para a criatividade, para a utilização de estratégias metodológicas como a resolução de
problemas, para a abordagem interdisciplinar, para o estabelecimento de relações entre os diferentes
campos matemáticos. Esse modelo de planejamento de ensino parece influenciar a aquisição de
conceitos matemáticos e contribuir para a evidência dos altos índices de dificuldades e de retenção em
disciplinas que envolvam cálculos, como a própria matemática.
É preciso enveredar por outros caminhos que possam substituir a linearidade. A idéia de uma estrutura
curricular diferente onde o conhecimento é organizado como rede de relações4, formando um
emaranhado de conceitos e classes de estímulos e respostas que se tornam equivalentes entre si, tem
se mostrado eficiente para o ensino e aprendizagem de uma diversidade de conteúdos matemáticos
(Rossit, 2003; Araújo, 2004; Reimberg, 2005).
No contexto nacional atual, com a expansão da noção de necessidades especiais, contemplando
dificuldades em diferentes níveis (Brasil, 2001), é importante tanto o desenvolvimento de variadas
metodologias de ensino como de procedimentos flexíveis de modo a atender a grande diversidade de
alunos. Assim, surge a preocupação com um processo de ensino-aprendizagem suficiente e eficaz que
atenda às necessidades educacionais para essa população em especial.
A Psicologia tem proporcionado contribuições no âmbito do ensino-aprendizagem. Uma das vertentes
que tem se preocupado com tal temática é a Análise do Comportamento, que se caracteriza pelo
estudo objetivo do comportamento dos organismos, levando em consideração o seu ambiente físico,
social, cultural e sua história como influências nas ações dos organismos.
A Análise do Comportamento humano, enquanto método científico, visa a previsão e controle do
comportamento. Para isso, o comportamento é investigado e variáveis são manipuladas visando o
entendimento de sua influência sobre tal comportamento. A partir de tais investigações, torna-se
possível desenvolver procedimentos de ensino para populações diferenciadas, como por exemplo, as
pessoas com deficiência mental. Sendo assim, ao conhecer as variáveis envolvidas no processo de
ensino-aprendizagem essas se tornam passíveis de manipulação e o comportamento almejado pode
ser instalado com maior controle.
Um planejamento, baseado na Análise do Comportamento, requer a análise de cada comportamento
e sua execução necessita de avaliação contínua, a fim de que decisões acerca da continuidade ou
redirecionamento do ensino sejam tomadas de acordo com a especificidade de cada caso (Rossit,
2004).
Ao planejar um método de ensino fundamentado nos princípios da análise do comportamento, deve-se partir do pressuposto que o repertório de conhecimento de cada indivíduo é único. Nesse sentido,
cabe ao educador investigar e conhecer o repertório de entrada dos alunos para que o ensino possa
ser planejado com vistas a atender às suas necessidades educacionais. O ensino deve ocorrer dos
elementos mais simples aos mais complexos. O grau de complexidade deve ser aumentado
gradativamente de acordo com as condições de aprendizagem, assim como, reduzir gradativamente os
níveis de apoio. A avaliação e o planejamento devem ocorrer de forma contínua e simultânea à
aplicação dos novos conteúdos. A aquisição de novas relações entre estímulos e entre estímulos e
respostas deve ser analisada através das respostas apresentadas na situação planejada de ensino. Se a
aprendizagem ocorrer, o educador poderá prosseguir com o seu planejamento, se houver
manifestações de dificuldades, o planejamento deve ser reavaliado e decisões devem ser tomadas no
sentido de redirecioná-lo ou redimensioná-lo.
4 Rede de relações é um conjunto de estímulos e desempenhos que mapeiam o território de equivalência de
estímulos (Stromer, Mackay, & Stoddard, 1992).
Essa proposta de organizar o ensino e avaliar a aprendizagem em rede de relações, ilustra como os
estímulos e as respostas se relacionam entre si, possibilitam uma economia de ensino, tendo em vista
que o educador, após mapear o repertório de entrada de seus alunos, irá intervir com bases sólidos
no ensino de novos conceitos e habilidades acadêmicas (leitura, escrita, matemática, ciências), pois
terá clareza quanto aos objetivos a serem ensinados.
Nesta estrutura diferente, as relações entre repertórios presentes e entre aqueles a serem adquiridos,
descartam a necessidade da presença de todos os pré-requisitos no repertório do indivíduo antes de
se introduzir um novo conteúdo. As relações são entendidas como coadjuvantes, ou seja, elas podem
ser ensinadas separadamente e aprendidas independentemente, propiciando a expansão da rede de
relações. Essa evidência, com relação ao processo de ensino-aprendizagem, indica que as relações
são independentes e que o ensino pode ocorrer a partir de qualquer relação, não sendo necessário
percorrer uma seqüência fixa (Rossit, 2003).
Essa concepção proporciona grandes benefícios para o ensino de pessoas com deficiência mental,
que apresentam características peculiares de aprendizagem, pois a partir da identificação das relações
presentes no repertório do indivíduo se insere gradativamente os novos estímulos que irão se
relacionar com o conhecimento já consolidado, expandindo a rede de relações e de conhecimento.
Assim o objetivo do presente estudo foi analisar a aquisição de relações matemáticas e apresentar o
currículo utilizado com deficientes mentais.
MÉTODO, RESULTADOS E DISCUSSÃO
ESTUDO I. Dez jovens com deficiência mental, idades de 12 a 32 anos, alunos em tempo parcial em
escola de Educação Especial, São Carlos-SP, ingressaram no estudo. O estudo foi conduzido em
uma sala da própria escola destinada exclusivamente para uso da pesquisa. O método de ensino foi
baseado em discriminação condicional com tarefas de escolha de acordo com o modelo, formação de
classes de equivalência e redes de discriminações condicionais, incluindo emparelhamento de
componentes e construção de respostas. Todas as tentativas de escolhas de acordo com o modelo
incluíram estímulos auditivos e visuais, apresentados por um computador, o qual também registrava e
salvava os resultados em arquivos.
Os estímulos experimentais foram numerais impressos (1, 5, 10, 25, 50 e 100), figura de moedas
apresentadas em cores e tamanhos originais e os respectivos valores numéricos e monetários ditados.
O pré-teste avaliou as habilidades de contagem, seqüência numérica, relações maior/menor, número
antes, depois ou igual, e habilidades monetárias para moedas, notas e preços impressos. Foram
apresentadas tarefas com material real sobre a mesa e outras apresentadas pelo computador. Após a
avaliação inicial, o treino foi iniciado com o primeiro participante. Quando este atingiu o critério de
90% de escolhas corretas, o treino foi introduzido para o segundo participante, e assim por diante. O
treino foi iniciado com a relação de identidade numeral impresso-numeral impresso, seguido do
emparelhamento do numeral ditado com numeral impresso e valor monetário ditado com figura de
moeda. Em seguida, os participantes foram testados para verificar a emergência de relações de
equivalência: moeda com numeral impresso e numeral impresso com moeda. O treino seguinte
consistiu do emparelhamento de estímulos compostos (1+1+1+1+1) com o numeral impresso
correspondente ao resultado da operação de adição e, então testado em tarefas de construção de
respostas sobre a mesa com valores monetários ditados e moedas verdadeiras. Testes de
generalização foram conduzidos com materiais e valores diferentes em situação de compra simulada.
Durante a compra simulada o participante deveria selecionar moedas de um conjunto e compor o
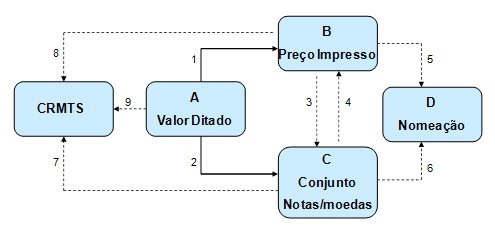
valor correspondente ao preço impresso no item a ser adquirido. A Figura 1 ilustra a primeira rede de
relações.
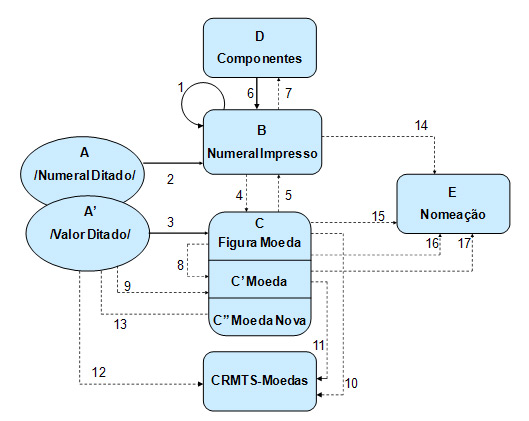
Figura 1. Rede de relações condicionais que compõe o currículo matemático para aquisição do comportamento de
manusear dinheiro. As caixas indicam os estímulos. As linhas cheias indicam as relações treinadas diretamente e as
tracejadas indicam as relações testadas. Os números mostram a seqüência de treino e teste.
Os resultados do pré-teste indicaram que cinco dos participantes apresentaram desempenhos
semelhantes com escores elevados, e os outros cinco apresentaram maiores dificuldades. As maiores
dificuldades estiveram relacionadas à contagem de objetos em seqüência, nomeação de moedas,
notas e preços, construção de respostas a partir do estímulo modelo moeda real ou valor monetário
ditado. Nas tarefas apresentadas pelo computador as menores porcentagens de acerto foram para as
tarefas de emparelhar conjuntos com numeral impresso, numeral impresso com figura de moeda e
vice-versa, emparelhar preço impresso com moedas e notas, e na tarefa de emparelhar estímulo
composto com numeral impresso. O treino da relação de identidade numeral impresso/numeral
impresso foi desempenhada com critério por todos os participantes. Os participantes P1 a P6
apresentaram no repertório de entrada a relação entre numeral ditado e impresso. A relação valor
ditado com figura de moeda foi introduzida, e rapidamente eles estabeleceram a relação. A relação
entre estímulos compostos e o numeral impresso foi adquirida por somente pelos participantes P1 a
P6. Nas sessões de testes os desempenhos com escores mais baixos ocorreram nas tentativas de
construção de resposta tanto com a figura da moeda como para o valor ditado como amostra. Os
participantes P7 e P8 necessitaram de revisões constantes de treinos anteriores e de diversos
procedimentos adicionais para adquirirem as relações. Os dois últimos participantes, P9 e P10, que
coincidentemente apresentaram escores mais baixos no pré-teste, não adquiriram as relações entre os
estímulos da classe dos numerais e do valor ditado, apesar dos diversos procedimentos adicionais de
ensino introduzidos. Concluiu-se que P1 a P6 adquiriram as habilidades monetárias via procedimento
de escolha de acordo com o modelo, incluindo emparelhamento arbitrário, treino de componentes e
resposta construída. De três relações treinadas diretamente, onze novas relações emergiram, o que
confirma a economia. Para mais da metade dos participantes, os que apresentaram melhor
desempenho no pré-teste, o procedimento foi eficaz. Para os demais, entretanto, aqueles que
mostraram desempenhos mais baixos no pré-teste, o procedimento foi mais longo para produzir
efeitos similares. As relações entre numeral impresso, figura de moedas, moeda verdadeira, assim
como, o desempenho na construção de respostas emergiram sem treino direto para aqueles que
apresentaram melhor desempenho no pré-teste e treino. Considerando que a rede de relações
condicionais envolvida no treino de habilidades monetárias é complexa e extensa e as características
da aprendizagem de pessoas com deficiência mental, é importante entender quais são os efeitos de
uma dada relação sobre a emergência de outras e assim, identificar melhores caminhos para ensinar
habilidades numéricas e monetárias para esta população.
ESTUDO II. Com o intuito de expandir a rede, um outro conjunto de relações complementa o
currículo inicial, com o objetivo de analisar a aquisição da relação entre figura de moeda-preço
impresso e de conjunto de moedas-preço impresso e avaliar o desempenho emergente em tarefas de
construção de respostas. Participaram deste seguimento do estudo sete dos dez jovens com
deficiência mental, que finalizaram a primeira parte do currículo. Nesse momento do estudo, as
seguintes habilidades estavam presentes no repertório desses jovens: emparelhar números e moedas
com seus correspondentes ditados; nomear moedas; emparelhar estímulos idênticos; emparelhar
estímulos compostos com o número impresso equivalente. As sessões foram conduzidas através de
um computador, que apresentava os estímulos, registrava e salvava os resultados em arquivos. Os
estímulos experimentais foram as figuras de moedas (1¢, 5¢, 10¢, 25¢ e 50¢), conjuntos de duas, três
e cinco moedas para os valores de 5, 10, 15, 20, 25, 30 e 50 centavos e preços impressos. As
relações treinadas e testadas estão na Figura 2.
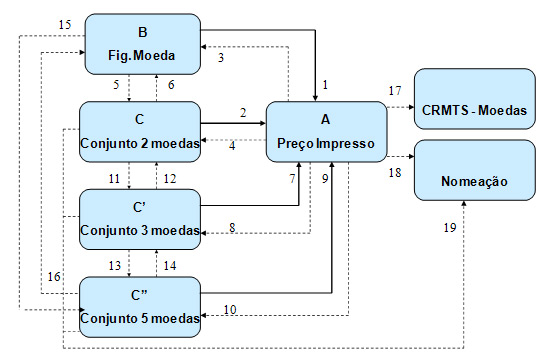
Figura 2. Rede de relações condicionais que expande o currículo matemático para aquisição do comportamento de
manusear dinheiro. As caixas indicam os estímulos. As linhas cheias indicam as relações treinadas diretamente e as
tracejadas indicam as relações testadas. Os números mostram a seqüência de treino e teste.
Os resultados demonstraram que de quatro relações ensinadas diretamente, treze novas relações
emergiram provavelmente em função do treino. Também foram verificadas oito relações que
generalizaram para condições diferentes, nas quais foram utilizadas moedas reais, valores monetários
não treinados e conjuntos de moedas diferentes das utilizadas no treino; e para situação diferente,
neste caso a compra simulada. O ensino através de escolha de acordo com o modelo mostrou-se
eficiente para a emergência da construção de respostas para os cinco participantes que completaram
as etapas de treino e testes. Outros dois participantes apresentaram maiores dificuldades na aquisição
das relações condicionais, necessitando de diversos procedimentos adicionais. Os resultados apontam
para a eficácia e eficiência do procedimento de ensino, visto a aquisição de habilidades complexas
num período de tempo reduzido, quando comparado com o tempo de vida e de escolarização. Um
dos aspectos importantes no ensino de pessoas com deficiência mental é a possibilidade de dotá-los
com habilidades que permitam atuar de forma independente na comunidade.
Os participantes com deficiência mental formaram classes extensas de estímulos equivalentes
derivadas de treinos anteriores, as quais foram generalizadas para valores não treinados e situação
simulada de compra. Além disso, é importante salientar que é possível estender ainda mais essas
classes por meio do acréscimo de novos estímulos às classes já existentes.
Tendo obtido resultados importantes na aquisição e generalização de relações condicionais complexas
na população em estudo, decidiu-se avançar na formação e expansão das classes de equivalência no
comportamento matemático, com o ensino de novas relações.
ESTUDO III. A expansão do currículo matemático envolveu a inclusão de novas relações e novos
estímulos. Cinco dos participantes, que concluíram a rede de relações da Figura 2, permaneceram
nessa etapa do estudo. Os estímulos experimentais foram numerais impressos 1, 5, 10, 25, 50 e 100,
figuras e conjuntos de notas, conjunto composto por notas e moedas, preço impresso e os respectivos
valores ditados. O ambiente experimental e os procedimentos de ensino permanecem os mesmos
descritos para as duas redes anteriores. A rede de relações foi ampliada substituindo-se os estímulos
moedas por notas (Figura 3) e apresentando estímulos compostos por notas e moedas
simultaneamente a serem relacionados com o preço impresso ou ditado (Figura 4).
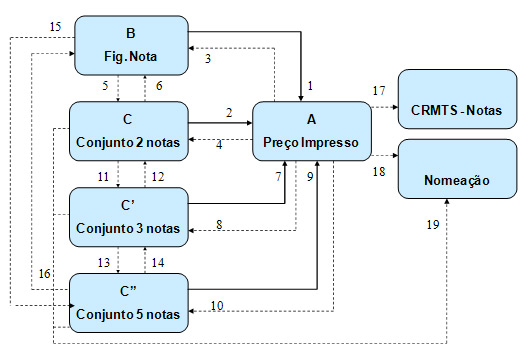
Figura 3. Rede de relações condicionais que expande o currículo matemático para aquisição do comportamento de
manusear dinheiro. As caixas indicam os estímulos. As linhas cheias indicam as relações treinadas diretamente e as
tracejadas indicam as relações testadas. Os números mostram a seqüência de treino e teste.
Figura 4. Rede de relações condicionais que completa o currículo matemático para aquisição do comportamento de
manusear dinheiro. As caixas indicam os estímulos. As linhas cheias indicam as relações treinadas diretamente e as
tracejadas indicam as relações testadas. Os números mostram a seqüência de treino e teste.
Analisando-se o currículo construído e ilustrado pelas Figuras 1 a 4, a formação e a expansão da rede
de relações ocorreu passo-a-passo. No total doze relações foram treinadas diretamente e 58 relações
testadas entre simetria, transitividade e generalização para estímulos, valores e situação diferentes. Em
média, foram necessárias 44 sessões de aproximadamente dez minutos cada, para que os
participantes completassem o treino e demonstrassem a formação de seis classes de equivalência (1,
5, 10, 25, 50, 100) com onze conjuntos de estímulos (palavras ditadas, numerais impressos,
componentes numéricos, valores ditados, moedas, conjunto de moedas, preços, moedas novas, notas,
conjunto de notas, conjunto de notas e moedas), além da emergência da nomeação e da construção
de respostas para 23 novos valores. Testes foram aplicados imediatamente após o treino e follow-up
após três e seis meses para avaliar a manutenção das relações no repertório dos participantes.
Os resultados demonstraram a eficácia do currículo informatizado sugerido e dos procedimentos de
ensino utilizados, constatada a aquisição de habilidades complexas num período de tempo reduzido
quando comparado ao tempo de vida e de escolarização e a manutenção das relações adquiridas ao
longo do tempo. Uma ampla e complexa rede de relações matemáticas foi ensinada a partir do treino
direto de apenas algumas dessas relações. A informatização do ensino agilizou o processo de ensino-aprendizagem, aumentou a confiabilidade dos dados e controlou as contingências, de forma a ensinar
exatamente conforme o planejado.
CONSIDERAÇÕES FINAIS
A Matemática está presente em diversas situações do cotidiano. Os números além de serem uma
linguagem de medida, eles também são necessários para os comportamentos adaptativos de encontrar
um endereço, usar um telefone, “ler” horas de um relógio, ou mesmo apreciar um jogo de futebol,
entre outros.
O objetivo do presente texto foi analisar a aquisição de relações matemáticas envolvidas no
comportamento de manusear dinheiro e apresentar o currículo, com a seqüência de treinos e testes,
utilizado com pessoas com deficiência mental que já acumulavam ao longo de sua vida pessoal e
acadêmica, histórias de baixo desempenho. Os resultados da seqüência de estudos mostraram que
participantes com deficiência mental formaram classes extensas de estímulos equivalentes e
expandiram para valores não treinados e situação simulada de compra. É importante salientar que é
possível estender ainda mais essas classes por meio do acréscimo de novos estímulos às classes já
existentes.
O currículo como rede de relações pautou-se no planejamento detalhado e na avaliação cuidadosa e
minuciosa de repertório inicial e das aquisições ao longo do processo de ensino e aquisição de novos
conhecimentos. O modelo aqui apresentado configura-se como uma estratégia promissora e viável de
ser aplicada em ambientes educacionais inclusivos, atendendo às necessidades educacionais de todos
os alunos. Cabe aos educadores, inteirar-se das inovações produzidas na área da Educação Especial
e aplicá-las nas salas de aula.
REFERÊNCIAS BIBLIOGRÁFICAS
ARAÚJO, P. Comportamento de subtrair com base no paradigma de equivalência de estímulos: um estudo com
deficientes mentais. São Carlos: UFSCar. Dissertação de Mestrado, 2004.
BRASIL. Parâmetros Curriculares Nacionais: Matemática/ Secretaria de Educação Fundamental. Brasília: MEC/
SEF, 1998.
BRASIL. Conselho Nacional de Educação/Câmara de Educação Básica (2001). Resolução CNE/CEB nº 2/2001.
Diário Oficial da União, Brasília, 14 de setembro de 2001. Seção 1E, p. 39-40.
CARMO, J. S. Aquisição do conceito de número em crianças pré.escolares através do ensino de relações
condicionais e generalização. Dissertação de Mestrado. Centro de Filosofia e Ciências, 1997.
DE LEON, N. P. A. Aquisição de habilidades básicas de matemática através da formação de equivalência em
crianças pré-escolares. Dissertação de Mestrado. São Carlos: UFSCar, 1998.
GREEN, G. Stimulus control technology for teaching number/quantity equivalences. Proceedings of the Conference
os the National Association for Autism (Austrália). Melboume: Vistoria Autistic Children´s, & Adults´
Association, Inc., 1992. p.51-64.
KAHHALE, E. M. S. P. Comportamento matemático: formação e ampliação do conceito de quantidade e relações de
equivalência. Tese de Doutorado, Instituto de Psicologia da Universidade de São Paulo, 1993.
MONTEIRO, G., & MEDEIROS, J. G. A contagem oral como pré-requisito para a aquisição do conceito de número
com crianças pré-escolares. Estudos de Psicologia, 7(1), 73-90, 2002.
MEDEIROS, J. G., HAYDU, V. B., CARMO, J. S., & ROSSIT, R. (2002). Ensino e aprendizagem de matemática:
contribuições do paradigma de equivalência de estímulos In: I Anais do Congresso de Psicologia, Ciência e
Profissão, São Paulo.. São Paulo: Art 3, v.1. p.118, 2002.
PIRES, C. M. C. Currículos de matemática: da organização linear à idéia de rede. São Paulo: FTD, 2000.
PRADO, P. S. T. O conceito de número: uma análise na perspectiva do paradigma de rede de relações. Dissertação
de Mestrado. São Carlos: Universidade Federal de São Carlos, 1995.
PRADO, P. S. T. Ensinando o conceito de número: contribuições do paradigma de rede de relações. Tese de
Doutorado. São Paulo: Universidade de São Paulo, 2001.
REIMBERG, K. Manuseio de dinheiro relacionado com a operação de subtração: estudo com deficiente mental. São
Carlos: UFSCar. Trabalho de Graduação. Departamento de Matemática, 2005.
RESNICK, L. B., WANG, M. C., & KAPLAN, J. Task analysis in curriculum design: A hierarchically sequenced
introductory mathematics curriculum. Journal of Applied Behavior Analysis, 6, 679-710, 1973.
ROSSIT, R. A. S. Matemática para deficientes mentais: contribuições do paradigma de equivalência de estímulos
para o desenvolvimento e avaliação de um currículo. TESE DOUTORADO. São Carlos:EDUFSCar, 2003.
ROSSIT, R. A. S., & FERREIRA, P. R.S. Equivalência de estímulos e o ensino de pré-requisitos monetários para
pessoas com deficiência mental. Temas em Psicologia da SBP, 2003a.
ROSSIT, R. A. S. Ensino de deficientes mentais: avaliação e planejamento In: PRIMEIROS PASSOS em Análise do
Comportamento e Cognição.1 ed.Santo André - SP : ESETec. Editores Associados, v.2, p. 89-98, 2004.
SPRADLIN, J. E., COTTER, V. W., STEVENS, C., & FRIEDMAN, M. Performance of mentally retarded children on
prearithmetic tasks. American Journal of Mental Deficiency, 78, 397-403, 1974.
STODDARD, L. T., BRADLEY, D. P., & MCILVANE, W. J. Stimulus control of emergent performances: teaching
money skills. In J. A. Mulick, & R. F. Antonak (Eds). Transitions in Mental Retardation. Vol.2. Issues in
Therapeutic Intervention Norwood, N.J: Ablex Publishing Co., p. 113-149, 1987.
STODDARD, L. T., BROWN, J., HURLBERT, B., MANOLI, C., & MCILVANE, W. J. Teaching money skills through
stimulus class formation, exclusion and component matching methods: Three case studies. Research in
Developmental Disabilities, 10, 413-439, 1989.
STROMER, R., MACKAY, H. A., & STODDARD, L. T. Classroom applications of stimulus equivalence technology.
Journal of Behavioral Education, 2, 225-256, 1992.
TEBEROSKY, A. & TOLCHINSKY, L. Além da alfabetização: a aprendizagem fonológica, ortográfica, textual e
matemática. São Paulo: Editora Ática, 2002.